MCMC for marketing data
The other day I was looking at marketing spend broken down by channel and wanted to compute some simple uncertainty estimates. I have data like this:
| Channel A |
|---|
| Channel B |
| Channel C |
| Channel D |
Of course, it’s easy to compute the cost per transaction, but how do you produce uncertainty estimates? Turns out to be somewhat nontrivial. I don’t even think it’s possible to do a t-test, which is kind of interesting in itself.
Let’s make some assumptions about the model:
- The cost per transaction is an unknown with some prior (I just picked uniform)
- The expected number of transaction is the total budget divided by the (unknown) cost per transaction
- The actual observed number of transactions is a Poisson of the expected number of transactions
I always wanted to try using pymc and now I had an excuse. See gist below:
The result in the form of an animated GIF (Unfortunately animated gifs were never widely accepted as a homework format back in school)
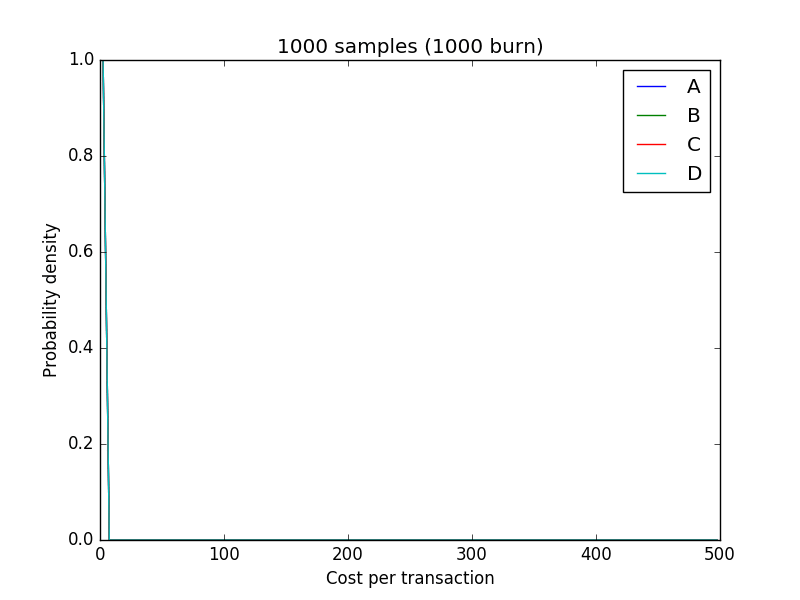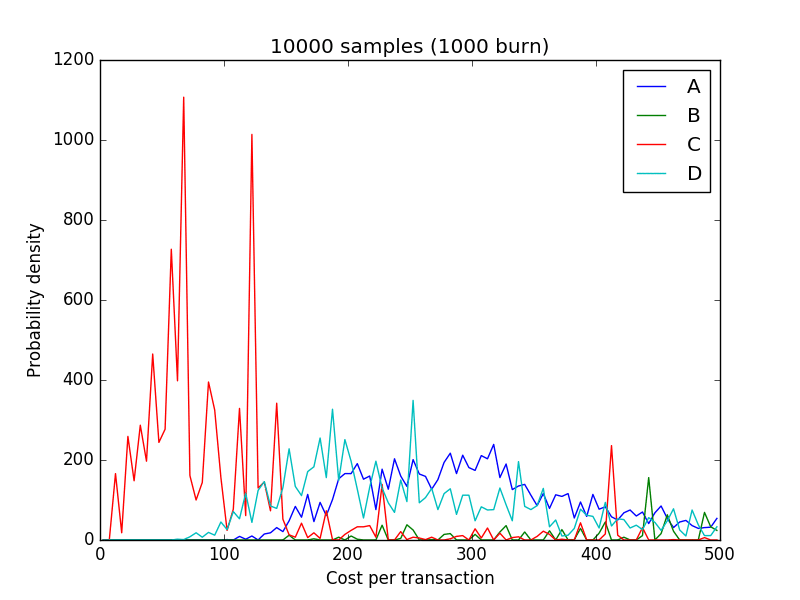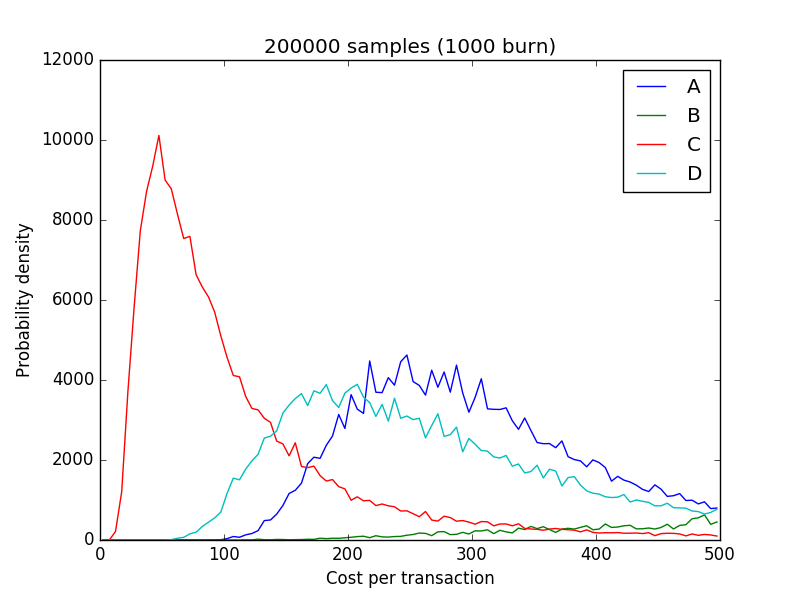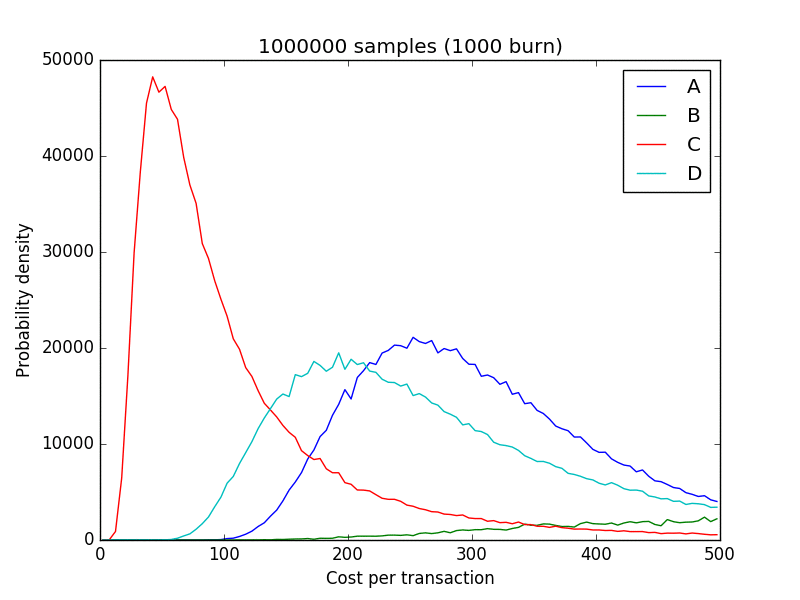
You even get a useless graph for free!
Of course, we could have computed this exactly, but I know myself and I’m very unlikely to get the expressions right without some serious effort. The conjugate prior of a Poisson is a Gamma distribution and we have to account for the parameterization of the cost per conversion as the budget divided by the total conversions, which will be another factor. How fun is that? I don’t have access to any windows to write on, so unfortunately not so fun.

From A Beautiful Mind
Anyway – this particular example might not have been the most useful example of using PyMC, but I do quite like the idea of it. Especially applied to conversion analyses, since it translates directly into a generative model. I will definitely use it for some further funnel analysis – in particular when the number of data points is very small and the model is very complex.
Tagged with: statistics