Fun with trigonometry: the world's most twisted coastline
I just spent a few days in Italy, on the Ligurian coast. Even though we were on the west side of Italy, the Mediterranean sea was to the east, because the house was situated on a long bay. But zooming in even more, there were parts of the coast that were even more twisted – to the point where it had turned a full 360 degress so you ended up having the sea to the west again.


Anyway, that made me curious – what’s the world’s most twisted coastline? If you trace the coastline along the Eurasian landmass, and keeps track of its direction, does it ever turn more 360 degrees? 720 degrees? 1040 degrees? Or, in radians, $$ 2\pi, 4\pi, 8\pi \ldots $$?
The data
You can download coastline data from OpenStreetMap. It turns out it’s not perfectly joined, so I ended up using the land polygon data instead. The slight drawback is that larger islands/continents are broken down into many polygons. Should not make an enormous difference. All in all there’s 587,205 distinct land polygons, each with a few hundred to thousands of vertices.
The math
I have something weird to admit. I actually kind of enjoy trigonometry. Let’s review some basic facts. Each land polygon is closed, and the sum of all the exterior angles adds up to roughly $$ 2\pi $$ radians. This is basic geometry:
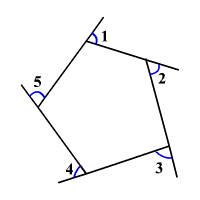
Why not exactly $$ 2\pi $$? We’re on a sphere, i.e. a non-Euclidean geometry. In those places, classic theorems are no longer true. Luckily, the curvature of the Earth is not substantial at a smaller scale, so we don’t have to worry about it.
I’m using pyshp to read the data. First step is to convert lon/lat to unit vectors in 3D, which I find far easier to work with:
def ll_to_3d(lat, lon):
lat *= math.pi / 180
lon *= math.pi / 180
x = math.cos(lat) * math.cos(lon)
z = math.cos(lat) * math.sin(lon)
y = math.sin(lat)
return numpy.array([x, y, z])
I did something similar when I computed a world map of ping latencies.
The only other magic sauce is that we need to compute the exterior angle or how much we “turn” when we go from vector $$ \mathbf{a} $$ to vector $$ \mathbf{b} $$ and then turn towards vector $$ \mathbf{c} $$. When $$ \mathbf{a, b, c} $$ are close to each other on the surface, you can ignore the curvature of the earth and think of them as just sitting on a plane. We want to know the exterior angle between $$ \mathbf{b-a} $$ and $$ \mathbf{c-b} $$. Turns out we can exploit the property of the cross product.
$$ \left| \mathbf{u} \times \mathbf{v} \right| = \left| \mathbf{u} \right| \left| \mathbf{v} \right| \mathbf{n} \sin \theta $$
where $$ \theta $$ is the angle. The vector $$ \mathbf{n} $$ is a unit vector pointing out of the earth if the turn is clockwise, and into the earth if it’s counter clockwise. We can figure that out by taking the dot product with $$ \mathbf{b} $$ (which is a unit vector and should be essentially parallel to the cross product). Not quite done yet. $$\sin^{-1}$$ only returns a value within $$ \left[ -\pi/2, \pi/2 \right] $$. We need to handle turns that are bigger than this as well. So we need a separate case for when the turn is so sharp that it’s going “backwards”. See code:
def mag(v):
return numpy.dot(v, v)**0.5
def spherical_angle(a, b, c):
n_sin_theta = numpy.cross(b-a, c-b) / (mag(b-a) * mag(c-b))
alpha = math.asin(numpy.dot(n_sin_theta, b))
if numpy.dot(b-a, c-b) >= 0:
return alpha
else:
return numpy.fmod(2*math.pi - alpha, 2*math.pi) - math.pi
It was easy to verify that it works – for polygons with thousands of edges it still returns an exterior angle sum very close to $$ 2\pi $$.
There’s a bit more work to take the series of cumulative angles and normalize it so that we can compute deviations. The whole script ended up being less than 100 lines so another example of a blog post being longer than the underlying script. (Eg. see the Language pitch post).
The results
I applied a bit of discretion when reviewing the results. The top 2 most winded coastlines are some swamp in UK. Google maps doesn’t line up with the Openstreetmaps data and so I disqualified these entries and a few more.
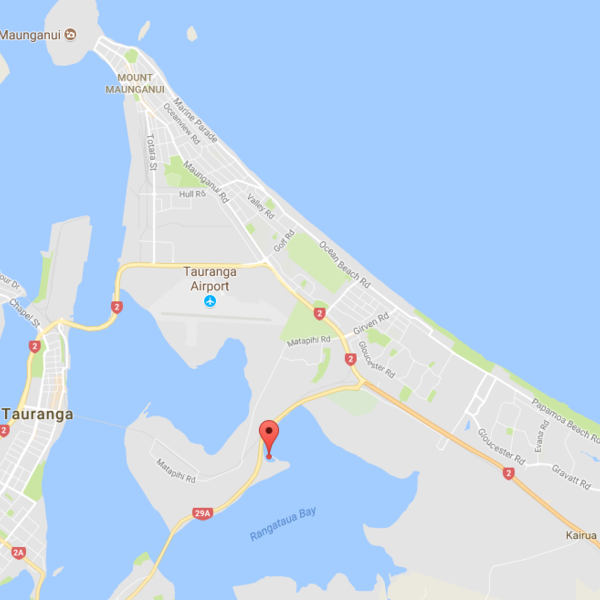
The most twisted coastline is just outside Tauranga, New Zealand:
The second most is in South Australia, seemingly in the middle of nowhere.
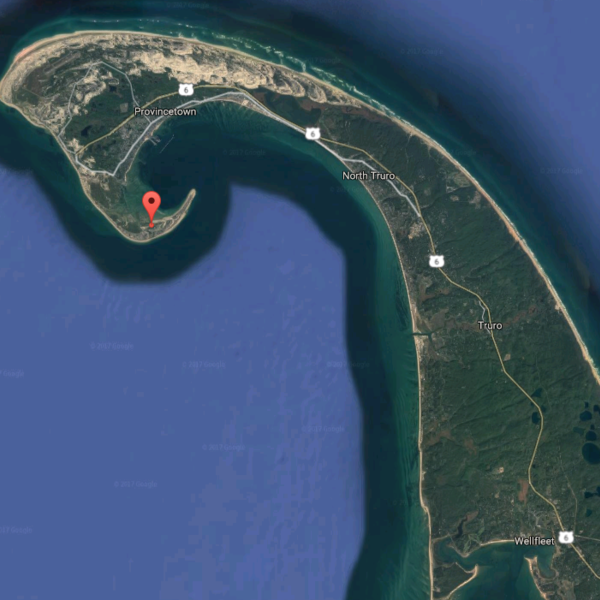
The third most is on Cape Cod, MA, which is amazing because I sort of expected Cape Cod to rank pretty high. Although Openstreetmap and Google have pretty different coastlines so honestly the exact location seems a bit unclear:
#4 is some random place in Nova Scotia, Canada
Top 20
I removed a whole bunch of these entries due to ambiguous coastlines – basically whenever Openstreetmaps didn’t align with Google:
| GM | OSM | Lat/Long | Where |
|---|---|---|---|
| GM | OSM | -37.6940, 176.2087 | Tauranga, New Zealand |
| GM | OSM | -34.6407, 135.3727 | Australia |
| GM | OSM | 42.0246, -70.1844 | Cape Cod, USA |
| GM | OSM | 45.9493, -60.5767 | Nova Scotia, Canada |
| GM | OSM | 1.9901, -157.4740 | Kiribati |
| GM | OSM | 32.9330, 129.7944 | Nagasaki, Japan |
| GM | OSM | 43.5846, 145.3271 | Hokkaido, Japan |
| GM | OSM | 54.2867, 13.6907 | Rügen, Germany |
| GM | OSM | 34.5192, 10.5364 | Tunisia |
| GM | OSM | 26.4628, -82.0632 | Cape Coral, USA |
| GM | OSM | 34.6861, 137.2857 | Tokyo, Japan |
| GM | OSM | 47.2325, -53.9598 | Newfoundland, Canada |
| GM | OSM | 55.1082, 10.0945 | Funen, Denmark |
| GM | OSM | 35.2210, -75.6807 | North Carolina, USA |
| GM | OSM | 46.8320, -64.0313 | Prince Edward Island, Canada |
| GM | OSM | 64.9621, -51.5111 | Nuuk, Greenland |
| GM | OSM | 55.2200, -7.7219 | County Donegal, Ireland |
| GM | OSM | 66.0704, -23.1252 | Ísafjörður, Iceland |
| GM | OSM | -43.8452, -176.4251 | Chatham Islands, New Zealand |
| GM | OSM | 52.2898, -174.3173 | Atka, Alaska, USA |
Notes
- Obviously the polygon resolution matters – coastlines are fractal and the higher resolution, the more twists you get.
- I was surprised that the twistedness was so small, even for the most extreme points. The top one was about $$ 4\pi $$, i.e. two full turns.
- I actually suspect the largest twistedness is still bounded. Even if we could measure with infinite precision, it might be an infinite series with a sum that converges.
- All code is on Github, as usual.