Bagging as a regularizer

One thing I encountered today was a trick using bagging as a way to go beyond a point estimate and get an approximation for the full distribution. This can then be used to penalize predictions with larger uncertainty, which helps reducing false positives.

To me it sounds like a useful trick that I found roughly 0 hits on Google for, so I thought I'd share it. Of course, it might be that I've completely gotten something backwards (my ML skills have some notable gaps), so let me know if that's the case.

Here's a little toy model to illustrate the idea. Let's assume we have observations $$ x_i $$ which are $$ mathcal{N}(0, 1) $$ . We also have $$ y_i = 0.2 + 0.3 / (1 + x_i^2) $$ and labels $$ z_i $$ sampled from the Bernoulli distribution given by $$ P(z_i=1) = y_i $$ (i.e. just flipping a weighted coin where the odds are determined by $$ y_i $$ .

Gradient Boosted Decision Trees are among the state of the art in regression and classification and can have amazing performance. They are available in scikit-learn and easy to plug into an existing script.

Let's say we want to find the best choices for $$ x $$ that gives large values of $$ y $$ . For instance, maybe we have click data and we want to find what items will get most clicks. We fit a GBDT to the $$ (x_i, z_i) $$ observations to train a model that predicts whether an item is going to get clicked or not based on the value of $$ x $$ .

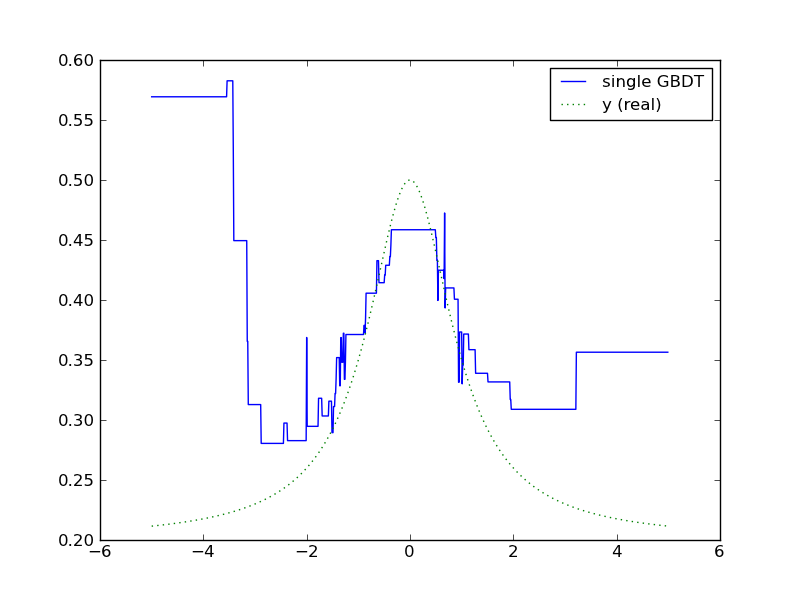
Unfortunately, we might end up getting wild predictions. In this particular case, a single noisy point in the training data around $$ x_i=-4 $$ makes the model believe that large negative values of $$ x $$ are good for maximizing $$ y $$ .

Here's the trick. Instead of training a single GBDT, we train 100 smaller GBDT's on strongly subsampled data (instead of 1000 data points, we sample 100 with replacement). Now, we can use all the predicted values of each GBDT to give us an idea of the uncertainty of of $$ y $$ . This is awesome, because (among other things) we can penalize uncertain estimates. In this case, I just picked the value at the 20th percentile. I have to confess I'm still a little unsure whether the distribution of $$ y $$ represents a probability distribution, but I think this is just an example of bootrapping and you could also Bayes rule with a prior to derive a posterior distribution.

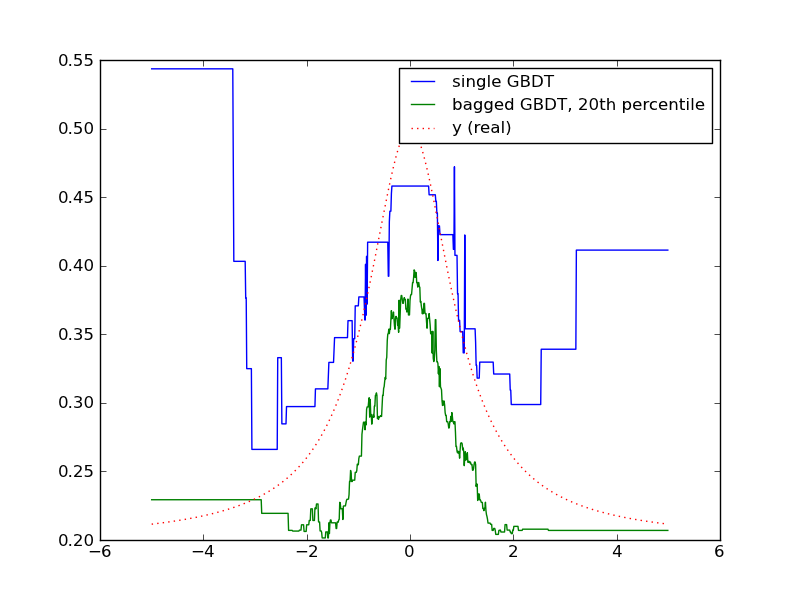
Why could this be useful? For instance, when we recommend music at Spotify, it's much more important to err on the safe side and remove false positives at the cost of false negatives. If we can explicitly penalize uncertainty, then we can focus on recommendations that are safe bets and have more support in historical data.