Detecting corporate fraud using Benford's law

Note: This is a silly application. Don't take anything seriously.

Benford's law describes a phenomenon where numbers in any data series will exhibit patterns in their first digit. For instance, if you took a list of the 1,000 longest rivers of Mongolia, or the average daily calorie consumption of mammals, or the wealth distribution of German soccer players, you will on average see that these numbers start with “1” about 30% of the time. I won't attempt at proving this, but essentially it's a result of scale invariance. It doesn't apply to all numerical series, like IQ or shoe size, but this pattern turns out to pop up in a lot of places.

Since the theory predicts that the first digit follows a certain outcome, you can use it to find “strange” distributions that seem to disobey what we can expect statistically. The Wikipedia article mentions using Benford's law to detect accounting fraud, and Greece was busted by researchers noting that the Greek macroeconomic data had an abnormally large deviation from what Benford's law would predict. There's another couple of papers and an interesting blog post applying Benford's law to industry sectors.

For fun, I downloaded about 5,000 annual reports (10-K) for most publicly traded companies in the US, to see if there are big outliers.

Benford's law predict that the probability of any first digit, 1-9, is

$$ Q(d) = left(log (d+1) - log d right) / log 10 $$ .

For every annual report, I calculate the empirical distribution, $$ P(d) = n_d / sum n_i $$ where $$ n_d $$ is just the number of occurrences of a dollar amount starting with digit d. To correct for reports with few values, I smooth the measured digit distribution a bit and add $$ 100cdot P(d) $$ “fake” counts to each $$ n_d $$ .

To measure the difference between expected and actual distributions, I use the KL-divergence which boils down to

$$ D_{P \mid Q} = sum_i log left( P(i) / Q(i) right) P(i) $$

I downloaded the annual reports from SEC and extracted all figures from all tables containing dollar amounts. Since some amounts may occur many times, and skew the digit distribution, I only looked at the unique amounts that occurred in the report. I then extracted first non-zero digit of all amounts.

The distributions of digits for the top five outlier entries illustrate Benford's law in practice:

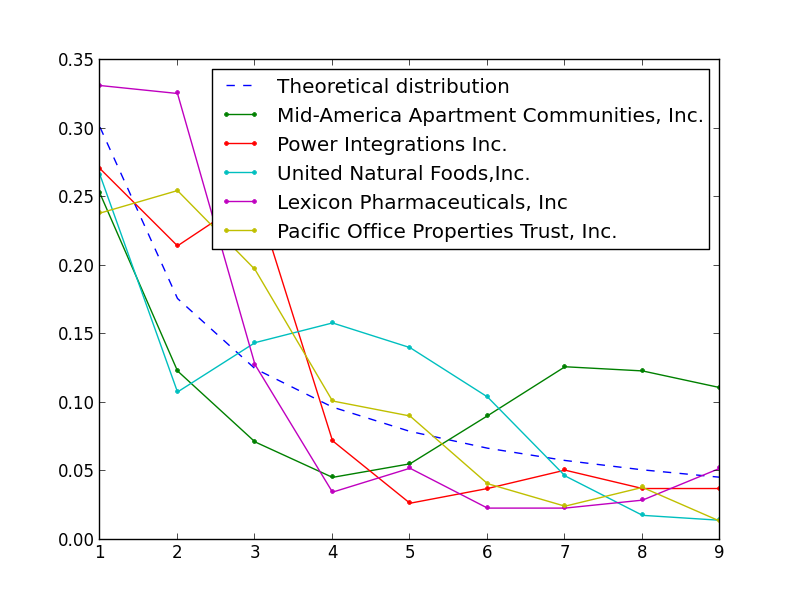
On closer inspection, some of these seem legit. For instance, the #1 spot on the list, Mid-America Apartment Communities, Inc. has a long list of units across the country, and the average price per unit happens to cluster around $800.

Below is a list containing the 100 companies with the largest KL-divergence (most “fishy”). None of the companies stand out as having an outrageous distribution, and even the top companies on the list are very unlikely to have commit fraud. The prior belief of accounting fraud is basically extremely low. We would commit the prosecutor's fallacy for singling out any of these numbers as fraudulent. Anyway, I'll follow up with a new blog post in five years to see if any of the companies below were actually caught:

<td>
  Mid-America Apartment Communities, Inc.
</td>

<td>
  Power Integrations Inc.
</td>

<td>
  United Natural Foods,Inc.
</td>

<td>
  Lexicon Pharmaceuticals, Inc
</td>

<td>
  Pacific Office Properties Trust, Inc.
</td>

<td>
  Xilinx
</td>

<td>
  Host Hotels & Resorts Inc.
</td>

<td>
  World Acceptance Corp
</td>

<td>
  Immunomedics, Inc.
</td>

<td>
  Marriott International Inc.
</td>

<td>
  CVS Caremark Corporation
</td>

<td>
  Paychex, Inc.
</td>

<td>
  Luna Innovations Incorporated
</td>

<td>
  Capstead Mortgage Corporation
</td>

<td>
  Verso Paper Corp.
</td>

<td>
  Fastenal Co.
</td>

<td>
  Insperity, Inc.
</td>

<td>
  Diamond Hill Investment Group Inc.
</td>

<td>
  National Security Group Inc.
</td>

<td>
  GameStop Corp.
</td>

<td>
  Compass Minerals International Inc.
</td>

<td>
  SIRIUS XM Radio Inc.
</td>

<td>
  BP Prudhoe Bay Royalty Trust
</td>

<td>
  Investors Bancorp Inc.
</td>

<td>
  Kohlberg Capital Corporation
</td>

<td>
  Equity One
</td>

<td>
  Kona Grill Inc.
</td>

<td>
  Alliance Financial Corporation
</td>

<td>
  Zale Corporation
</td>

<td>
  Anadarko Petroleum Corporation
</td>

<td>
  Sigma-Aldrich Corp.
</td>

<td>
  Global Cash Access Holdings, Inc.
</td>

<td>
  Corcept Therapeutics
</td>

<td>
  Enbridge Energy Management LLC
</td>

<td>
  BJ's Restaurants Inc.
</td>

<td>
  Air Transport Services Group, Inc.
</td>

<td>
  Fairchild Semiconductor International Inc.
</td>

<td>
  Universal Electronics Inc.
</td>

<td>
  Espey Manufacturing & Electronics Corp.
</td>

<td>
  Inland Real Estate Corporation
</td>

<td>
  W. R. Berkley Corporation
</td>

<td>
  Albemarle Corp.
</td>

<td>
  Koss Corp.
</td>

<td>
  Leap Wireless International Inc.
</td>

<td>
  Encore Wire Corp.
</td>

<td>
  UQM Technologies, Inc.
</td>

<td>
  DuPont Fabros Technology Inc.
</td>

<td>
  Applied Materials Inc.
</td>

<td>
  Destination Maternity Corporation
</td>

<td>
  Pepsico, Inc.
</td>

<td>
  CorVel Corporation
</td>

<td>
  Nathan's Famous Inc.
</td>

<td>
  Sport Chalet, Inc.
</td>

<td>
  Key Technology Inc.
</td>

<td>
  Overhill Farms Inc.
</td>

<td>
  Digi International Inc.
</td>

<td>
  Materion Corporation
</td>

<td>
  DreamWorks Animation SKG Inc.
</td>

<td>
  NIC Inc.
</td>

<td>
  ANSYS Inc.
</td>

<td>
  Volterra Semiconductor Corporation
</td>

<td>
  Verenium Corporation
</td>

<td>
  KeyCorp
</td>

<td>
  Rockwell Collins Inc.
</td>

<td>
  Meritage Homes Corporation
</td>

<td>
  Perrigo Co.
</td>

<td>
  Zhone Technologies Inc
</td>

<td>
  McGrath RentCorp
</td>

<td>
  A.M. Castle & Co.
</td>

<td>
  Delta Natural Gas Co. Inc.
</td>

<td>
  Pervasive Software Inc.
</td>

<td>
  Senomyx
</td>

<td>
  ManTech International Corp.
</td>

<td>
  Ross Stores Inc.
</td>

<td>
  Bancorp Of New Jersey, Inc.
</td>

<td>
  Werner Enterprises
</td>

<td>
  Dillards Inc.
</td>

<td>
  Sparton Corp.
</td>

<td>
  Rudolph Technologies Inc.
</td>

<td>
  CyberOptics Corp.
</td>

<td>
  Hallador Energy Company
</td>

<td>
  DARA BioSciences, Inc
</td>

<td>
  Chico's FAS Inc.
</td>

<td>
  Delcath Systems Inc.
</td>

<td>
  Pure Cycle Corp.
</td>

<td>
  Cytori Therapeutics
</td>

<td>
  Vonage Holdings Corporation
</td>

<td>
  Spectranetics Corporation
</td>

<td>
  Regal-Beloit Corporation
</td>

<td>
  ScanSource, Inc.
</td>

<td>
  Weyco Group Inc
</td>

<td>
  Ambassadors Group Inc.
</td>

<td>
  Rent-A-Center Inc.
</td>

<td>
  Accenture plc
</td>

<td>
  Idenix Pharmaceuticals
</td>

<td>
  KAR Auction Services, Inc.
</td>

<td>
  Progressive
</td>

<td>
  BCSB Bankcorp Inc.
</td>

<td>
  PCTEL, Inc.
</td>

<td>
  Cincinnati Financial Corp.
</td>

Again, a bunch of disclaimers: this is just a silly application, don't take it seriously, elevator inspection certificate available in the building manager's office, etc.