The eigenvector of "Why we moved from language X to language Y"
I was reading yet another blog post titled “Why our team moved from <language X> to <language Y>” (I forgot which one) and I started wondering if you can generalize it a bit. Is it possible to generate a N * N contingency table of moving from language X to language Y?
Someone should make a N*N contingency table of all engineering blog posts titled "Why we moved from <language X> to <language Y>".
— Erik Bernhardsson (@bernhardsson) January 25, 2017
So I wrote a script for it. You can query Google from a script and get the number of search results using a tiny snippet. I tried a few different query strings, like move from <language 1> to <language 2>, switch to <language 2> from <language 1> and a few more ones. In the end you get a nice N * N contingency table of all languages:
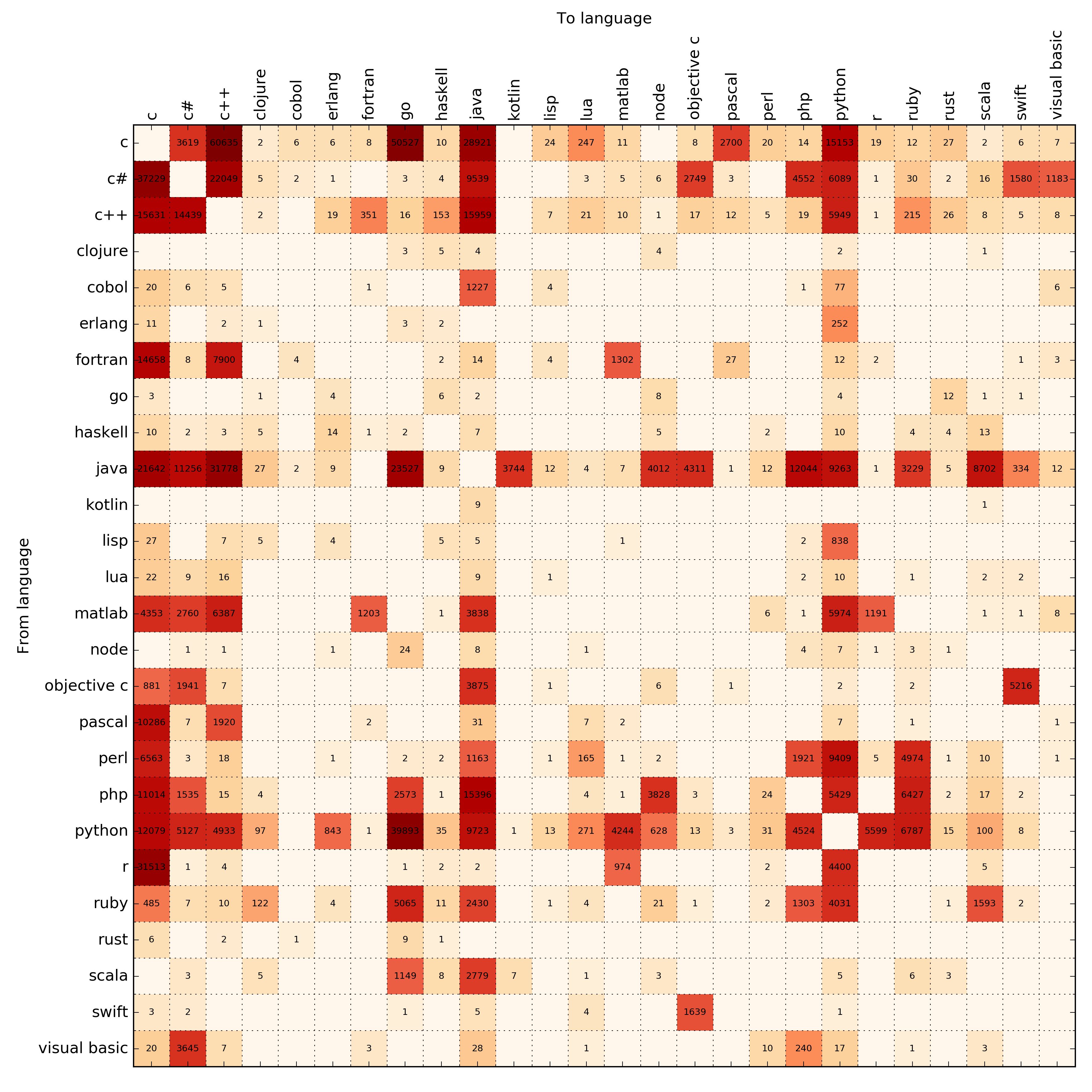
Here's where the cool part begins. We can actually treat this as probabilities from switching between languages and say something about what the future language popularities will be. One the key is that the stationary distribution of this process does not depend on the initial distribution – turns out this is basically just the first eigenvector of the matrix. So you really don't have to make any assumptions about what's popular right now – the hypothetical future stationary state is independent of this.
We need to make this into a stochastic matrix that describes the probabilities of going from state $$ i $$ to state $$ j $$. This is easy – we can interpret the contingency matrix as transition probabilities by just normalizing across each row – this should give a rough approximation of the probability of switching from language $$ i $$ to language $$ j $$.
Finding the first eigenvector is trivial, we just multiply a vector many times with the matrix and it will converge towards the first eigenvector. By the way, see notes below for a bunch of more discussion on how I did this.
Go is the future of programming (?)
Without further ado, here is the top few languages of the stationary distribution:
- 16.41%: Go
- 14.26%: C
- 13.21%: Java
- 11.51%: C++
- 9.45%: Python
I took the stochastic matrix sorted by the future popularity of the language (as predicted by the first eigenvector).
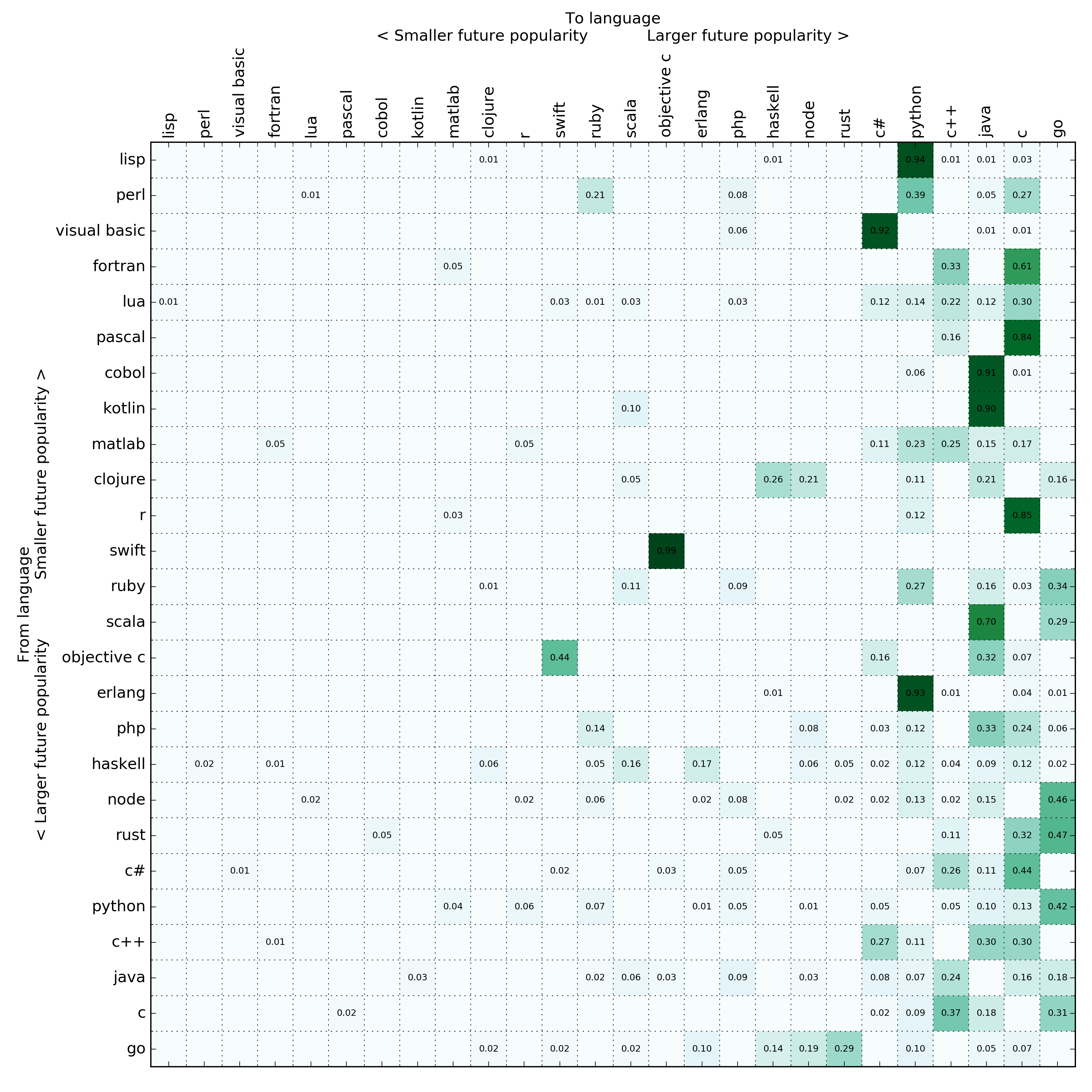
Surprisingly, (to me, at least) Go is the big winner here. There's a ton of search results for people moving from X to Go. I'm not even sure how I feel about it (I have mixed feelings about Go) but I guess my infallible analysis points to the inevitable conclusion that Go is something worth watching.
The C language, which turned 45 years old this year, is doing really well here. I did a bunch of manual searches and in many cases a lot of the results are really people writing about how they optimize certain tight loops by moving code from X to C etc. But is that incorrect? I don't think so. C is the lingua franca of how computer works and if people are still actively moving pieces of code to C then it's here to stay. I seriously think C will be going strong by its 100th birthday in 2072. With my endorsements for C on LinkedIn, I expect recruiters to reach out to me about C opportunities well into the 2050's (actually taking that back – hopefully C will outlive LinkedIn).
Other than that, the analysis pretty much predicts what I would expect. Java is here to stay, Perl is dead, Rust is doing pretty well.
Btw, this analysis reminds me of this old tweet
Very interesting graphing showing rate of switch between R and Python for data analysis pic.twitter.com/moYFgrHCBJ
— Big Data Borat (@BigDataBorat) April 24, 2014
Javascript frameworks
I did the same analysis for frontend frameworks:
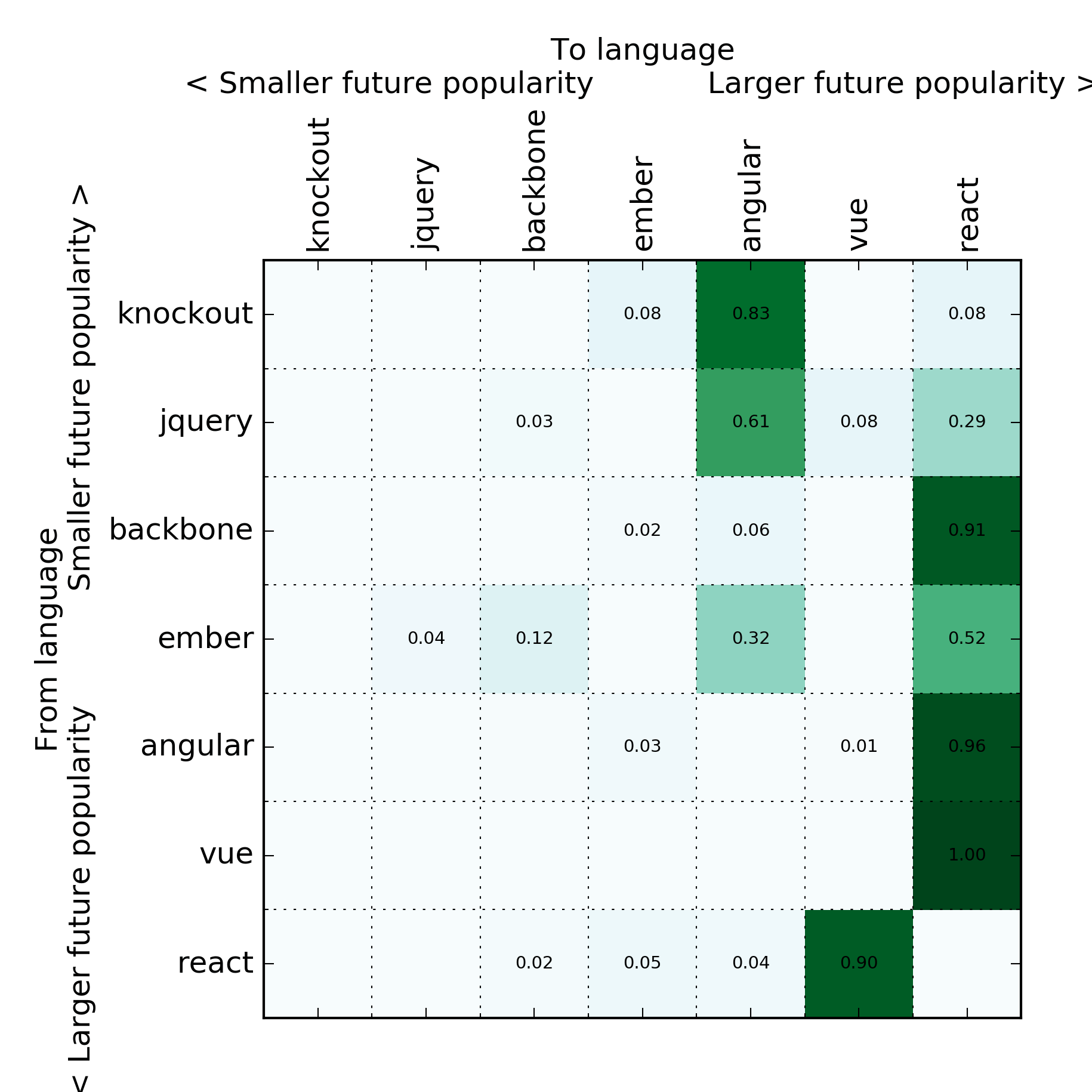
I expected React to come out on top here, but interestingly Vue is doing really well. I'm also surprised how well Angular stacks up – anecdotally it seems like a mass exodus away from it.
Databases
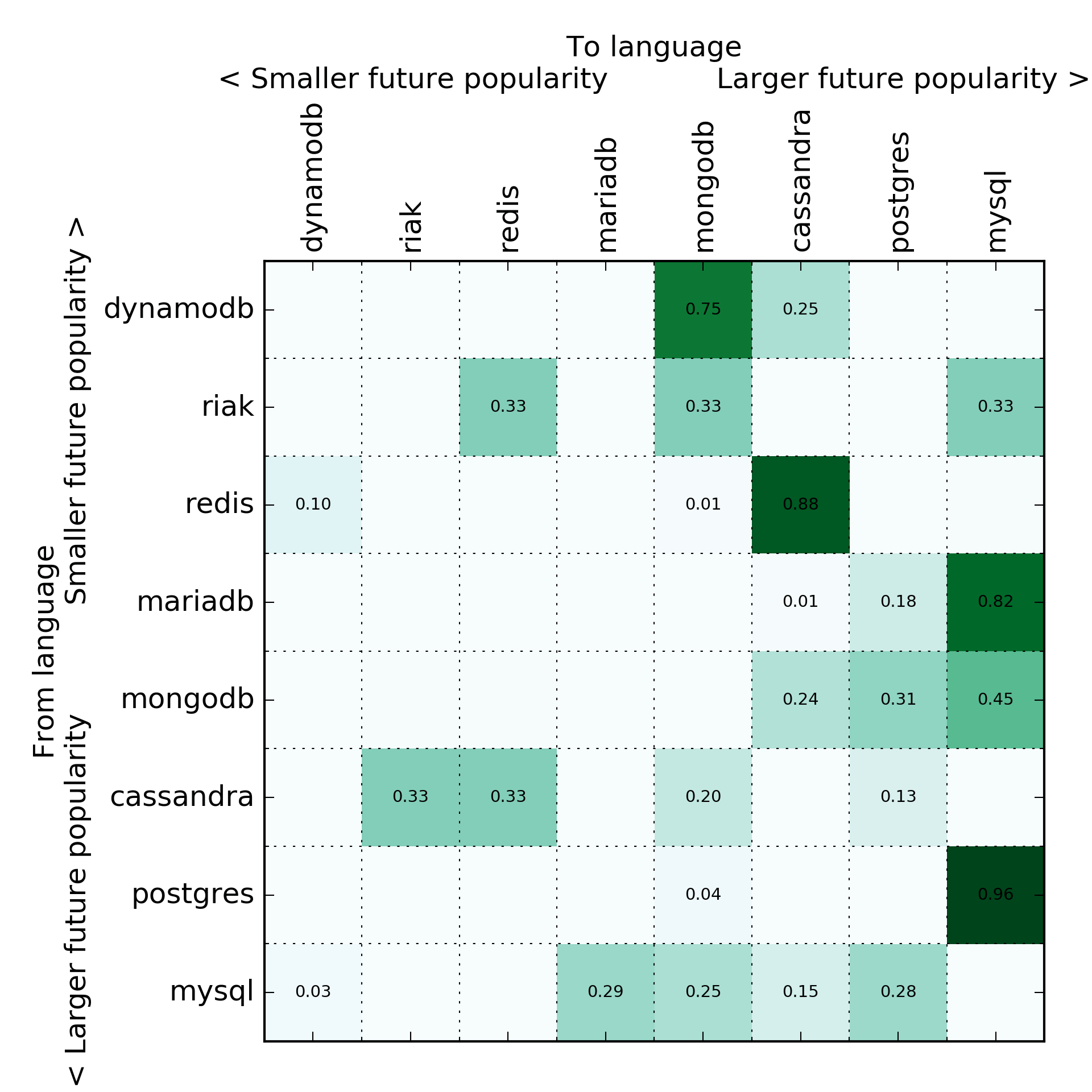
I started looking at ride sharing apps, deep learning frameworks, and other things, but the data is far more sparse and less reliable. Will keep you posted!
Notes/caveats
- See discussion on Hacker News and /r/programming
- This blog post was another inspiration: Why I switched from language 1 to language 2.
- Here's how to scrape Google and get the number of search results
- Unfortunately Google rate limits queries by IP, but I ended up using Proxymesh to scrape it for all the N * N combinations 🤓
- Note that I searched for exact queries by putting it in quotation marks: eg “switch from go to c++”
- The attentive reader might ask why Javascript wasn't included in the analysis. The reason is (a) if you are doing it on the frontend, you are kind of stuck with it anyway, so there's no moving involved (except if you do crazy stuff like transpiling, but that's really not super common) (b) everyone refers to Javascript on the backend as “Node”
- What about the diagonal elements? There is of course a really big probability that people just stay with a certain programming language. But I'm ignoring this because (a) turns out search results for things like stay with Swift is 99% related to Taylor Swift (b) the stationary distribution is actually independent of adding a constant diagonal (identity) matrix (c) it's my blog post and I can do whatever I want 🙉
- On (b), it is true that $$ e(\alpha S + (1-\alpha)I) = e(S) $$ where $$ e(\ldots) $$ denotes the first eigenvalue and $$ I $$ is the identity matrix. This doesn't exactly map to reality – the probability that you stay with a certain language may be different across languages.
- The method of repeated multiplications to get the first eigenvalue is called Power iteration.
- Is this model with eigenvectors a super-accurate description of reality? Probably not. The old quote by George Box comes to mind: All models are wrong, some are useful.
- I also know the chain has to be ergodic and a bunch of other things, but in reality that's basically always the case.
- Code is available on Github.