Waiting time, load factor, and queueing theory: why you need to cut your systems a bit of slack

I’ve been reading up on operations research lately, including queueing theory. It started out as a way to understand the very complex mortgage process (I work at a mortgage startup) but it’s turned into my little hammer and now I see nails everywhere.
One particular relationship that turns out to be somewhat more complex is the relationship between cycle time and throughput. Here are some examples of situations where this might apply:
- What’s a good CPU load for a database? If the CPU load is 50%, how much does that impact latency vs if CPU load is 25%?
- What’s the average time it takes to respond to an email as a function of how busy I am?
- What’s the relationship between the tech team’s throughput (in terms of Trello cards per day or whatever) and the cycle time (time from adding a card until it’s done)?
- If we need an loan to be underwritten in at most 2 days, how many underwriters do we need?
- I need to book a meeting with my manager. His/her calendar is 80% full. All meetings are 1h and s/he works 40h/week. How far out am I going to have to book the meeting?
- Same situation as above but I need to book a meeting with 5 people, all having 80% full calendars (that are independent of each other). How far out?
- Users file bugs to the developer. Assuming we put 1 developer full time on triaging/solving incoming bugs, and that keeps the person x% busy, what’s the time until a bug gets resolved?
In all these cases, it turns out that running a system at a lower throughput can yield dramatic cycle time improvements. For instance me being just “kind of busy” 😅 vs SUPER SWAMPED 😰 anecdotally impacts my email response time easily by 5-10x.
I’ve written about this in the past but in an almost mythical way – I didn’t understand the math behind these principles.
First of all, the relationship might seem nonsensical. If you have a garden hose, the throughput of the hose (liter/s water) is completely independent of the cycle time (the length of the hose). If a database can handle 1000 queries per second, and we’re currently doing 500 queries/s (so 50% load), why is the latency higher than if we’re doing 100 queries/s (10% load?)
The reason, like much else in life, is variability. If the database can be thought of as a worker that can handle exactly one query at a time, there’s going to be a queue that at any time has any nonnegative number of queries in it. The number of queries sitting in the queue will vary over time. Due to chance, we might have a 10 queries that arrive at almost the same time. In that case the worker will have to process each query serially and work its way through the queue.
As it turns out, we can simulate this fairly easily using dynamic programming. Let’s say the time between queries are exponentially distributed and the time of the query itself is log-normally distributed (the exact distributions here aren’t super important, but there are some good reasons to model the world using those ones). You can simulate the whole system doing something like this:
query_enqueued = numpy.cumsum(numpy.random.exponential(
size=(n,), scale=1./k))
query_time = numpy.random.lognormal(size=(n,))
query_finished = numpy.zeros((n, ))
for i in range(n):
query_finished[i] = query_enqueued[i] + query_time[i]
if i > 0:
# Can't finish before the previous query finished
# plus the time for this query
query_finished[i] = max(
query_finished[i],
query_finished[i-1] + query_time[i])
If you run this snippet with different values for k and plot the latency as a function of load factor, you get a chart that’s super interesting (in my opinion!):
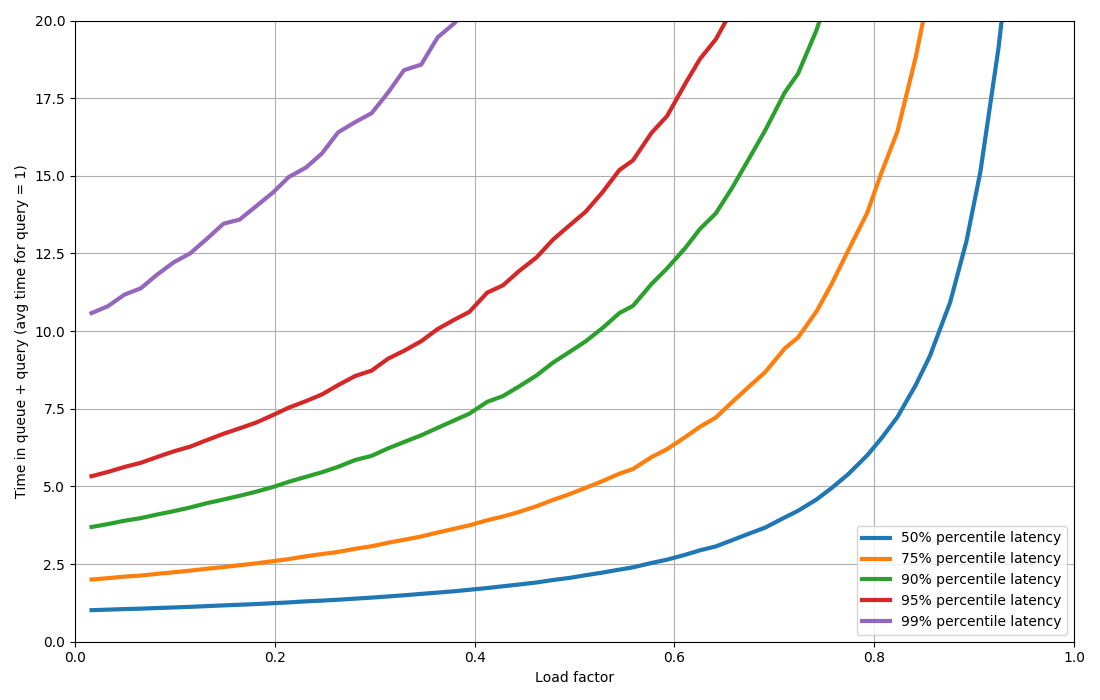
At 50% utilization, you get twice the latency that you do with 0% utilization. Once you start hitting say 80% utilization then it goes up. And it goes up FAST. Getting towards 100% utilization, the asymptote here is the vertical line.
If you want to optimize for higher-percentiles (such as 90th or 99th) then just a little bit of load pushes the latencies up a LOT. Basically you are forced to run the system at a really low load factor to have some leeway.
The system described above is called an M/G/1 using fancy notation. Turns out for a slightly simpler case where instead of a lognormal distribition, we have an exponential distribution (M/M/1), we can derive exact values for these latencies. The key observation is that the number of events in the queue will have a Geometric distribution. The mean ends up being $$ 1 / (1 - f) $$ where $$ f $$ is the load factor. But my mom told me not to trust equations on the internet, so let’s simulated it just to be on the safe side:
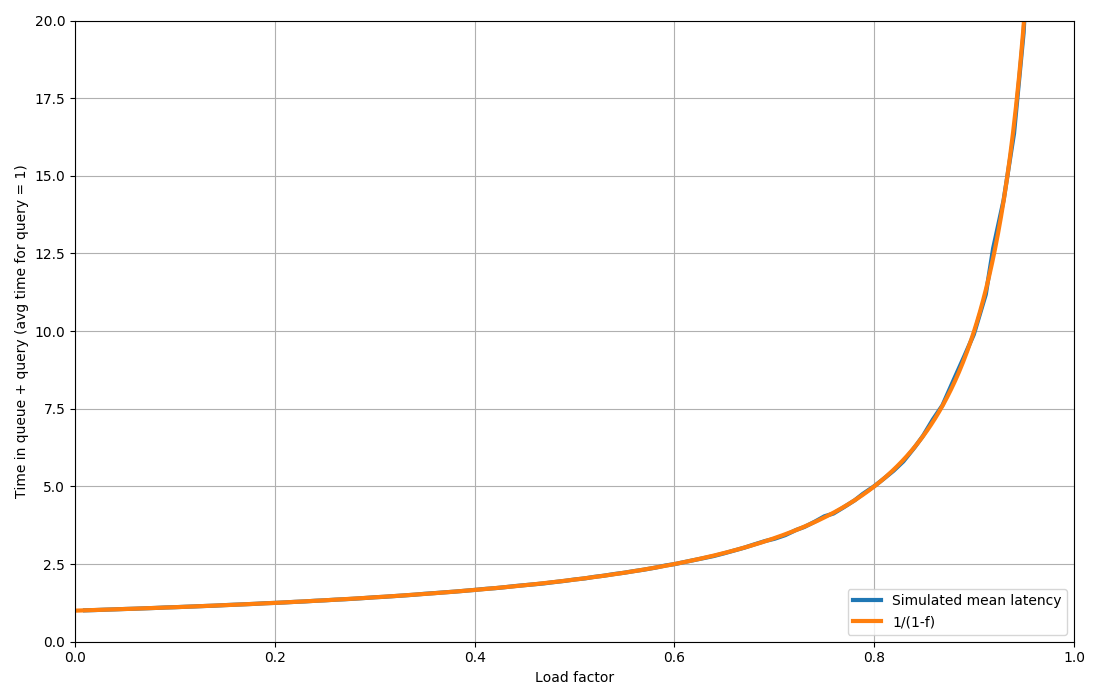
In case you can’t see, there are two lines exactly on top of each other 💯.
One use case – get more done and be less stressed
I talked a lot about this in a technical context but let’s switch gears a bit and allow me to put on my corporate philosopher hat. It’s a metaphorical hat that I like to wear, and when I wear it, I mutter things like: the speed at which a company innovates is fundamentally limited by the size of the iteration cycle. So what can you do to reduce the size of that cycle? The observation is that if I’m spending 100% of my time on super urgent stuff, all highest priority, then with fairly mild assumptions, that stuff will have an extremely long cycle time.
So how do we prevent that? Let’s split up work into “things that need to happen now” vs “things that can wait”. You really don’t want to spend 100% of your time being in the critical path for all the company’s major projects. It’s exactly the times when I’m stuck in “reactive mode” where my backlog of stuff builds up. Instead, make sure that a big chunk is important, but has no imminent deadline attached to it.
My strategy is to take all the urgent things, and delegate/automate it until the average load of “urgent things” is below 50%. It’s possible some of the output is marginally lower quality, but the upside is now I can improve the latency by an order of magnitude. I can respond to emails and Slack messages faster, I can find time for an unexpected meeting, etc, and more generally, information can propagate faster.
Other notes
- It makes sense to co-locate batch jobs with low-latency processing and let the latter take precedence at any time. In fact I think this was the intuition behind building Google Borg.
- It might seem like parallelization would help, but in fact it makes the problem even harder. A 2x faster machine with a single request queue will always have lower latency that two 1x machines with their own request queues. This in fact reminds me of a really old (2013) blog post that got widespread attention about Heroku’s routing.