How to hire smarter than the market: a toy model
Let's consider a toy model where you're hiring for two things and that those are equally valuable. It's not very important what those are, so let's just call them “thing A” and “thing B” for now. For one set of abilities, the scatter plot looks like this:
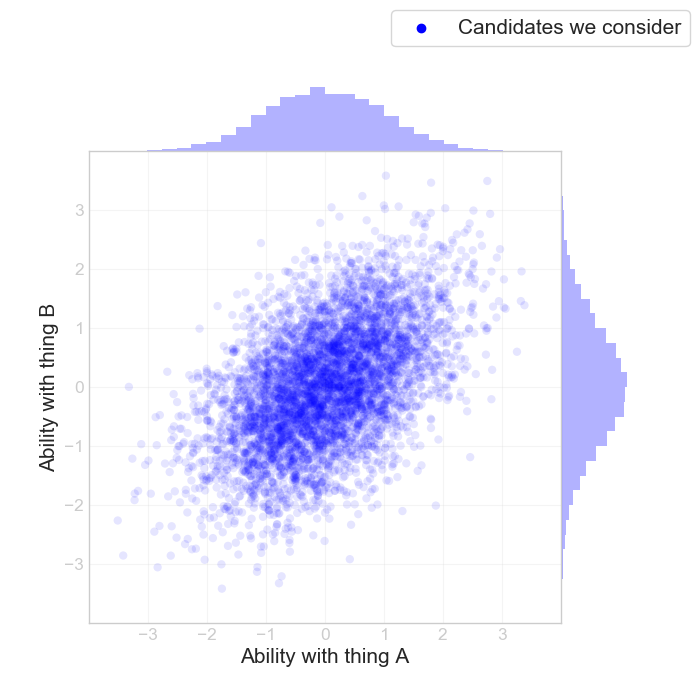
The assumption here is that A and B are drawn from a 2D-Gaussian with a mild positive correlation. I crammed a whole lot of stuff into this plot: the scatter plot shows the distribution of A vs B, and the two histograms (on top and on the right) shows the distribution over A and over B.
We're going to hire some people, so we look at a bunch of resumes and try to decide who's going to make it to the next stage. The best candidates are the ones that are great at both A and B, and we'll obviously bring them in. But some candidates are going to be good at A but not B, or vice versa. So you might choose to evaluate candidates on some combination of the two. For instance, bring in people for which $$ A + B > k $$ where $$ k $$ is some constant:
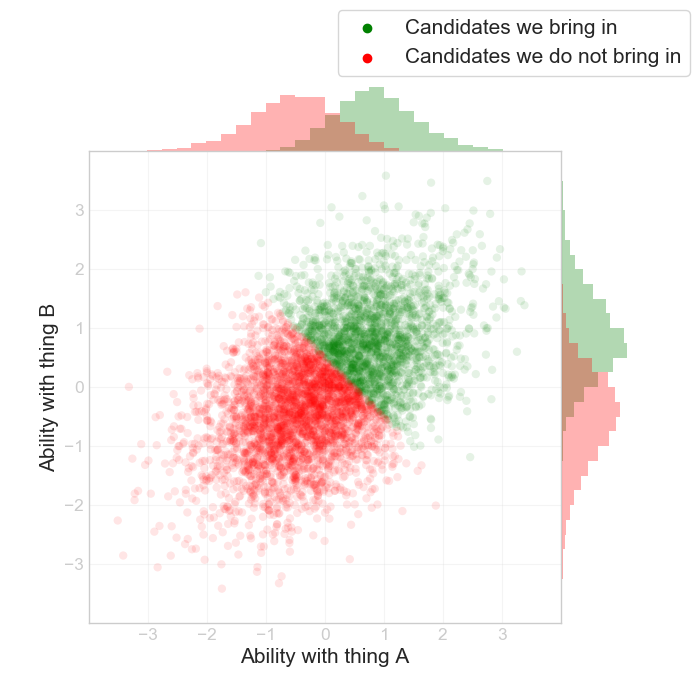
We can already see something interesting here, which is that the candidates we bring in exhibit a negative correlation between thing A and B, despite those being independent. This is something that's called Berkson's paradox.
I've written about a particular example of this previously: Google found that experience with programming competitions was negatively correlated with actual work success. This would happen if we relabel the x-axis above to say “general interview feedback” and the y-axis as “programming competition success”. The problem isn't that programming competition success is somehow bad: it might have a strongly positive correlation with future work performance. The problem is that Google probably overweighted programming competition success in their hiring process versus other things that would more accurately predict future work performance. This caused an “artificial” negative correlation between those two qualities among the group that were hired.
An interesting paper claims a negative correlation between sales performance and management performance for sales people promoted into managers. The conclusion is that “firms prioritize current job performance in promotion decisions at the expense of other observable characteristics that better predict managerial performance”. While this paper isn't about hiring, it's the exact same theory here: the x-axis would be something like “expected future management ability” and the y-axis “sales performance”.
This problem of overweighting is a consistent theme throughout this post and we'll get back to it!
It gets worse: the market forces
Because you're hiring in a market with many other players, the really good candidates may simply have so many options that they are going to go to whatever company they want to and make a zillion dollars. Let's say A and B are equally valued by you, as well as the market. We end up we something like this:
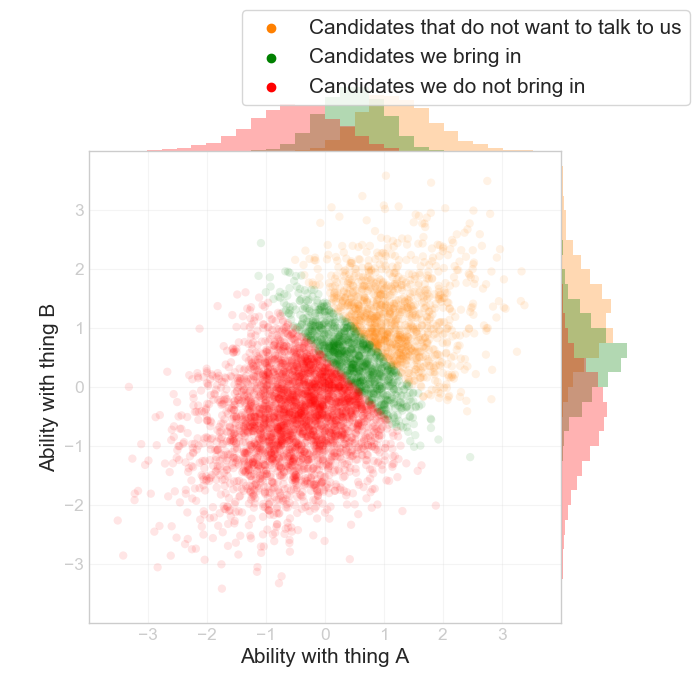
Look at the green segment here: now there's an even stronger negative correlation between A and B.
Recruiting is like buying a home
This isn't only for recruiting, and I think this negative correlation is intuitively more clear in the context of buying a home. You might value an extra bathroom as worth +$50,000, and an extra bedroom as +$100,000, but so does the market. As a result, given your budget, you'll see a negative correlation between having an extra bathroom and having an extra bedroom, because the market prices you out of having both.
But this also presents an opportunity. The tradeoffs forces you to focus on the things that you value more than the market. Maybe you don't think a 4th floor walk-up is more than a -$10,000 penalty for you, but the market values it as -$20,000: then in fact you should hone in and target exactly those apartments. As we will see with recruiting, the trick to figure out your own preference versus the market. Let's dig into a few cases.
A few case studies
A common human bias is to interpret confidence as a sign of competence, and as a first order approximation, let's say the market prices both equally. But let's assume that we decide we're not going to succumb to the same bias as the market as a whole. We conclude that the market overvalues confidence, and that we're going to do everything we can to eliminate this bias from our interviewing process. While competence isn't easy to observe, let's say we can get very close by having a carefully thought out interview process. The resulting chart is something like this:

Our cutoff is going to be a vertical line, since we only care about competence, not confidence. The “market cutoff” is going to be the diagonal line. The people we end up considering will be the green triangle.
Here's the weird thing though: our group of people that we consider will:
- On average have low confidence
- Exhibit a negative correlation with confidence and competence
The same phenomenon arises in more complex situation. Let's say everything else equals, it is better to hire someone from a fancy school, but that the market overvalues it. In contrast, let's say we value general competence slightly more than the market. The market cutoff will be a 45 degree line, but our cutoff will be a line with a different angle. We end up with something like this:
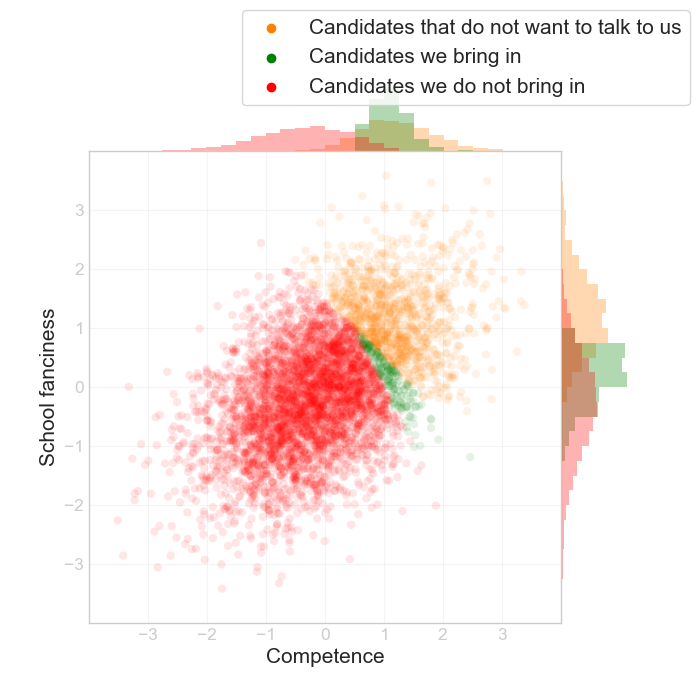
There's a similar conclusion here: we actually see that the candidates we're interested in went to a less than average fancy school.
More generally, the conclusion when you're hiring in a competitive market is that even if you think some quality is desirable, if you think the market overvalues that quality, you should look at the other side of the spectrum. This goes back to my example about buying a home.
A model for finding the best candidates
The model so far is easy to understand and helps us explore a few tradeoffs when hiring but I think it falls short in a few areas. Let's create a slightly more complex model that is a bit less intuitive but I think slightly more realistic. This section is a bit more math, so feel free to skip if it's not your thing.
What we really want to optimize for is our estimated value divided by the market's value since the market determines the salary, roughly. Assumptions:
- The value to the company is $$ v_c = \exp(\alpha_c x + \beta_c y) $$ where $$ (\alpha_c, \beta_c) $$ is a vector with parameters we pick
- The market value (i.e. the salary) is $$ v_m = \exp(\alpha_m x + \beta_m y) $$ where $$ (\alpha_m, \beta_m) $$ is a vector with parameters that the market values
- The quantity we're trying to optimize is $$ z = v_c / (v_m + k) $$ where $$ k $$ is a constant.
- The constant (which I set to $$ k = 1 $$) represents some combination of
- We don't want to just take the market price for candidates: we pay them a fair base wage that ramps up with market demand.
- The cost of hiring/onboarding/training.
Throughout the next few plots, let's set the “market vector” for all of them to $$ (\alpha_m, \beta_m) = (1, 1)$$ i.e. the market values the two things equally. We then vary how much we care about those things.
First of all, let's say we value A and B equally, but we care about them a bit less than the market. We bucket the candidates into three different buckets based on the value $$ z = v_c / (v_m + k) $$. If we plot this, we see the same negative correlation (the blue line):
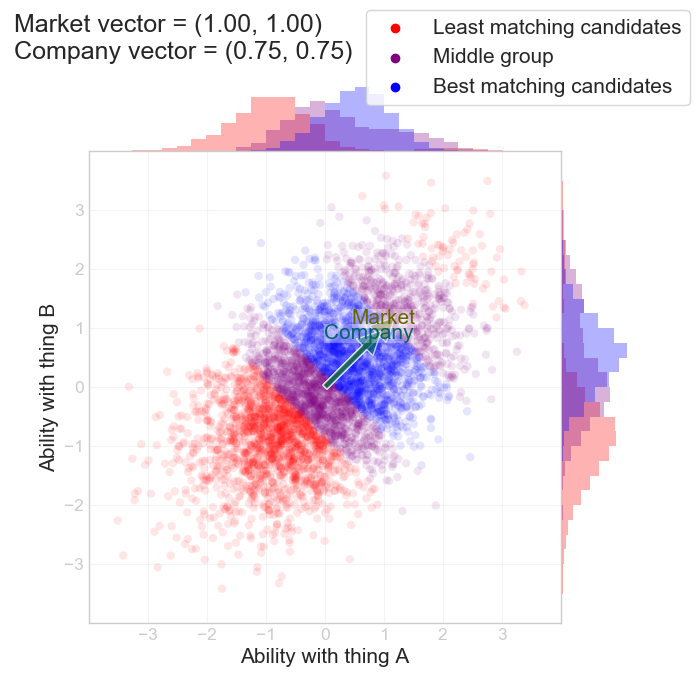
If we decide we're going to outbid the market we can set $$ (\alpha_c, \beta_c) = (2, 2) $$ on the other hand:
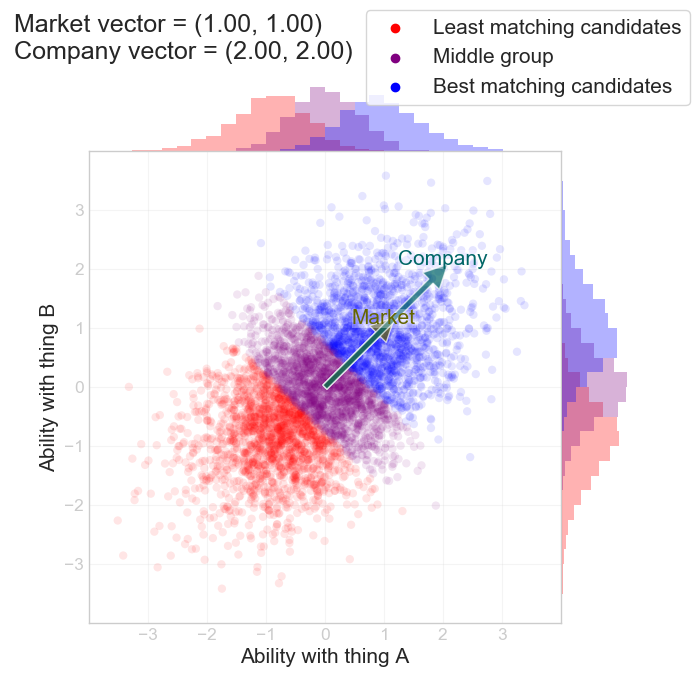
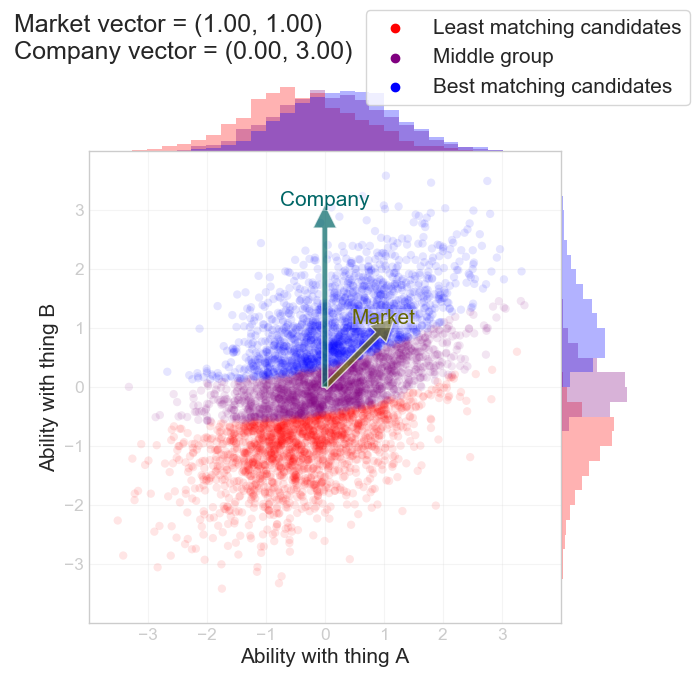
The more interesting things happen if we decide we don't care about quantity B, but the market still does. This would correspond to the competence-confidence case where the x-axis is competence and the y-axis is confidence. The market values both, but we are smarter and we only value the former. We set $$ (\alpha_c, \beta_c) = (1, 0) $$:
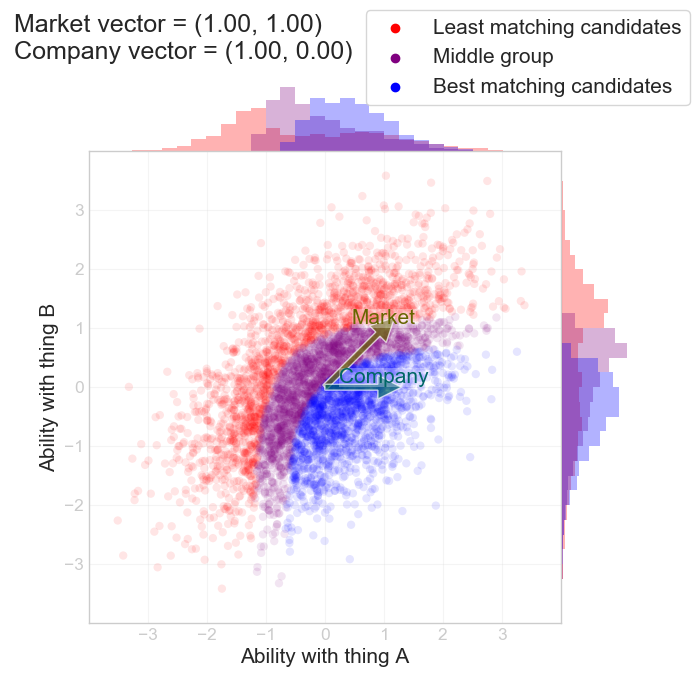
Similarly to what we saw earlier, we see that we if we go after the “best” people (in terms of the quantity $$ z = v_c / (v_m + k) $$ then we actually end up hiring the people that have less-than-average confidence. This is because the market systematically underprices those.
In the other case when we think thing A and B are both positive, but we think the market overvalues thing B, we can set $$ (\alpha_c, \beta_c) = (1, 0.5) $$. This would correspond to the example where A is the fanciness of the school they went to.
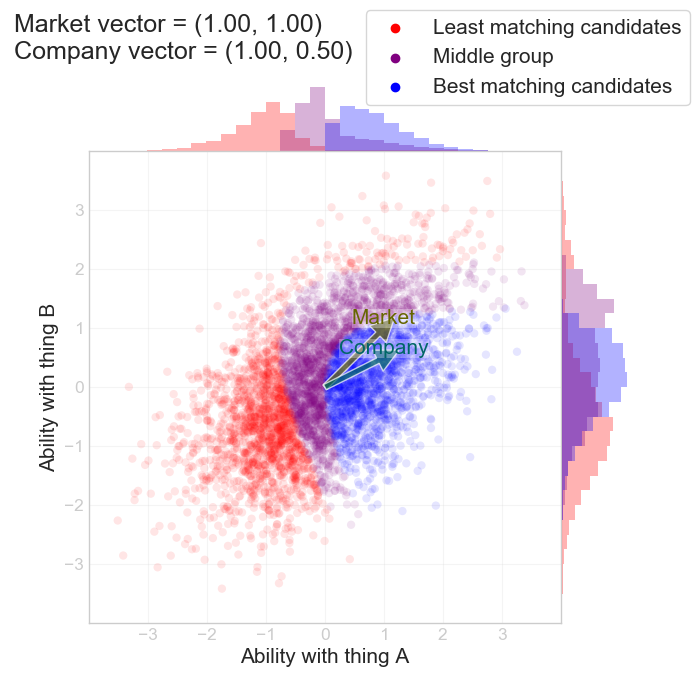
The outcome is somewhat similar. Even though we prefer candidates from fancy schools, we still end of being better off hiring people from “average” schools. Again, this is because the market systematically undervalues those. The fact that we consider B a “good” quantity is less relevant than the fact that we consider it less valuable than the market does.
A different case would be a company that only pays attention to some superficial measurement at the cost of things that matter more. For instance, let's say the x-axis is “task-relevant experience” and the y-axis is “fanciness of their degree”. This situation isn't so contrived: I've talked to recruiters at bigcorp enterprises, where there's a strong mandate to only hire Ph.D.‘s but where (my guess) the interview process is pretty noisy. We set $$ (\alpha_c, \beta_c) = (0, 1) $$:

The interesting observation is the histogram at the top: the blue distribution of hired candidates end up having a much lower task-relevant experience than the ones that were rejected. Not a hiring strategy I would endorse. There is however one odd twist to this. Let's say we keep ignoring feature A (task-relevant experience), but we throw all our money bidding out basically anyone else based on B (fanciness of their degree):
Because there's some small correlation between A and B, we actually do end up at this point getting higher-than-average skills in terms of A. The cost is that we're going to have to out-spend everyone else. A far more cost-conscious way would be instead to pay a medium premium for A and a small for B, rather than a huge for B but none for A.
Conclusions and opportunities
If you ask the average recruiter how they find people, it's usually some type of Boolean search on LinkedIn, and when you ask them how they grade resumes, it's typically some combination of having CS degrees from fancy schools, having the exact experience with the tech stack you have (down to frameworks), etc. God forbid if someone has a gap on their resume, or if they need visa sponsorship.
What my model implies, is that there's an “arbitrage opportunity” here. In fact, it's a bit of a silver lining to the fact that the market is biased. Are companies systematically putting a premium on something? Then bet against them! Go after the underdogs. If every hiring manager acts in their own rational self-interest (which unfortunately, they don't) then over time these biases will vanish and the market will converge towards efficiency.
You might have your own personal preferences here, and I'm not going to judge you, but here's a few thoughts on things that may be undervalued by the market:
- Candidates from non-fancy schools
- Candidates who didn't go to school at all and are self taught, or have some non-traditional path into the field
- Candidates who didn't get a CS degree
- Candidates who never worked at any well-respected company
- Candidates who are low confidence or “interview poorly”
- Candidates that could experience discrimination for other reasons, like being from an underrepresented groups, or not fitting some stereotype of what a software engineer should look like
- Candidates who need visa sponsorships
- Candidates who don't have experience with your exact tech stack, but a strong generalist foundation (this is especially prevalent in complex industries, which I tweeted something about this a few weeks ago)
- Candidates who left the workforce for a while to take care of family
- … many more things
I want to be extra clear about what my conclusion here is. I'm not saying you should think of it as a bad thing that someone is coming from a fancy school. Everything else equals, it's typically a good thing! What I'm saying is that if you're hiring, then you will be more successful going after candidates that the market undervalues. And this doesn't just apply to measurable things (what school they went to), but also things that people subconsciously value (eg. confidence of a candidate). On the other hand, overvaluing things (that are less predictive of future work performance) can lead you to hire worse candidates.
In all these cases, it turns out your preference versus the market's preference matters more than your preference in itself.
All of this stuff may or may not sound obvious to you!
Appendix
- I only talked about tradeoffs between two traits (A and B), but the model extends well into many more ones. But computer screens are two-dimensional and it's harder to plot more dimensions than 2!
- These models may seem a bit arbitrary to you, and of course every model is a somewhat arbitrary simplification of reality! I'm not claiming that it's perfect.
- That being said, both models gave the answer my intuition told me on basically the first attempt: the conclusions are very robust to the inputs, and I spent almost zero time trying to pick the right parameters.
- Even without the screening step and without a competitive market, you might still end up with a negative correlation for the people you make an offer to. I've mentioned this in the past talking about Pareto frontiers. It's a slightly different phenomenon, though.
- I don't mean to pick on recruiters, and there are some absolutely outstanding ones that I've worked with in my life!
- I accidentally published a draft of this a few days ago, sorry about that!
- The (very simple) code is on Github, as always.