Predicting solar eclipses with Python

As I am en route to see my first total solar eclipse, I was curious how hard it would be to compute eclipses in Python. It turns out, ignoring some minor coordinate system head-banging, I was able to get something half-decent working in a couple of hours.

I didn't want to go deep on celestial mechanics, so I decided to leverage Python's fantastic ecosystem for everything. The package Astropy turns out to have about 80% of the stuff I wanted, in particular making it quite straightforward to compute the position of the sun and the moon in the sky. After just a few minutes of googling, I had something that computes the overlap between the sun and the moon given a particular point on the Earth:

from astropy.coordinates import EarthLocation, get_body
from astropy.time import Time
from astropy.units import deg, m

def sun_moon_separation(lat: float, lon: float, t: float) -> float:
    loc = EarthLocation(lat=lat * deg, lon=lon * deg, height=0 * m)
    time = Time(t, format="unix")
    moon = get_body("moon", time, loc)
    sun = get_body("sun", time, loc)

    sep = moon.separation(sun)
    return sep.deg

This takes a (latitude, longitude) pair as well as a unix timestamp and computes the angular separation between the sun and the moon. Basically this means just the distance between the centers of the objects, seen in the sky from the Earth. If the angular separation is very close to zero, we have a solar eclipse.

However! I didn't want to compute this for a given coordinate. I wanted to compute the location of a total eclipse given a timestamp (if there is one).

Ideally, we would grab 3D coordinates for the Earth, the sun, and the moon. Then project a line between the sun through the moon, see if that line hits the Earth, and if it does, find the latitude and longitude of this intersection. This is probably the “right” way to do it, and if I had time, I would brush the dust off my geometry skills and do this.

However, I don't have time! It's the day before the eclipse, and I just want to compute coordinates in the least arduous way possible. We already have something that computes a related thing, but we need to flip things around a bit. We're going to do this using a bulldozer I love using for stuff like this: black-box optimization.

Solving for the coordinates using black-box optimization

We have a function that takes (timestamp, latitude, longitude) and outputs the distance between the sun and the moon in the sky. But let's instead try to solve this related problem: Given a timestamp, find the latitude and the longitude that minimizes the distance between the sun and the moon in the sky.

If the minimum distance is essentially zero, this means that we found a solar eclipse. In that case, the coordinate that minimizes the function is the center of the sun's shadow on the Earth.

It's relatively straightforward to minimize an arbitrary function like this. My go-to package for this is scipy.optimize which has a bunch of well-tested routines that are probably implemented in Fortran 77 if you dig deep enough. We don't even have the gradient for the function, but that's fine — Nelder-Mead is your friend.

The nice part of it is we can treat this function as a completely black-box and optimize it from the outside. It does get somewhat computationally expensive, but it's not something I would personally lose sleep over.

The code to use scipy.optimize.minimize to find the eclipse location ends up like this:

def find_eclipse_location(dt: datetime) -> tuple[float, float] | None
    """Return the coords of a total eclipse, or `None`."""
    t = datetime.timestamp(dt)
    fun = lambda x: sun_moon_separation(x[0], x[1], t)

    ret = minimize(fun, bounds=[(-90, 90), (-180, 180)], x0=(0, 0))
    return ret.x if ret.fun < 1e-3 else None

Basically, we bind the time to sun_moon_separation, and construct a new function with 2 variables: latitude and longitude. And then we search over this function (with bounds) to find the minimum.

This almost works! Well, part of the problem was that I wasted 2 hours because of a dumb sign error with latitudes and longitudes. But even after fixing that, I ended up with weird spurious coordinates.

I think this is because of bogus minima, since I think the the antipode of one solution is another solution. We should obviously discard solutions when you can't see the sun. Two simple modifications makes the solver work super reliably:

1. If the sun or moon is below the horizon, return some large number
2. Instead of using (0, 0) as the starting point, do a simple grid search over a few points on the Earth and pick the one with the smallest sun-moon distance. Then use that point as the starting point for the optimization.

My final code for sun_moon_separation and find_eclipse_location ends up just a tiny bit more complex than what I shared above. With these tricks, we now have a function that reliably takes any timestamp and figures out the latitude/longitude for a solar eclipse (if there is one).

Finding all the eclipses

Ok, so now let's find a bunch of eclipses! In particular, let's find the path of every eclipse in the 2020-2030 span. This will require us to search over a lot of timestamps.

Alas, the find_eclipse_location function is pretty slow!

So what do we do? More tricks:

1. Do a coarse search over the full decade, only probing every hour. If we identify an eclipse, do a more granular search and map out the path minute by minute.
2. Parallelize!!!

I'm the CEO of Modal, which makes it super easy to take Python code and run it in the cloud. Honestly I wasn't planning on using Modal for this, but scaling out computationally intensive functions is such an great use case for Modal that I immediately just grasped for it.

We can find all eclipses in the 2020-2030 period my adding a simple decorator to find_eclipse_location and then mapping over it. The mapping code ends up looking like this:

def run():
    dt_a = datetime(2020, 1, 1, 0, 0, 0, tzinfo=timezone.utc)
    dt_b = datetime(2030, 1, 1, 0, 0, 0, tzinfo=timezone.utc)

    # Compute evenly spaced datetimes
    dt = dt_a
    dts = []
    while dt < dt_b:
        dts.append(dt)
        dt = dt + timedelta(seconds=3600)

    # Map over it using Modal!!!
    for tup in find_eclipse_location.map(dts):
        if tup is not None:
            print("Found eclipse at", tup)

Plotting it

I'm glossing over a few details in the actual code, but bear with me. Once we have all the paths, we can plot them. I used Basemap and got something half-decent pretty quickly:

from matplotlib import pyplot
from mpl_toolkits.basemap import Basemap

def plot_path(dts: list[datetime], lats: list[float], lons: list[float]):
    # Set up a world map                                                                                                                                                                              
    pyplot.figure(figsize=(6, 6))
    lat_0, lon_0 = lats[len(lats) // 2], lons[len(lons) // 2]
    bm = Basemap(projection="ortho", lat_0=lat_0, lon_0=lon_0)
    bm.drawmapboundary(fill_color="navy")
    bm.fillcontinents(color="forestgreen", lake_color="blue")
    bm.drawcoastlines()

    # Plot eclipse path
    x, y = bm(lons, lats)
    bm.plot(x, y, color="red")

I added a few more things in my final script, including local times by using timezonefinder to look up local timezones from (latitude, longitude) pairs.

This is what the eclipse tomorrow (on 2024-04-08) looks like if we plot it using the script:

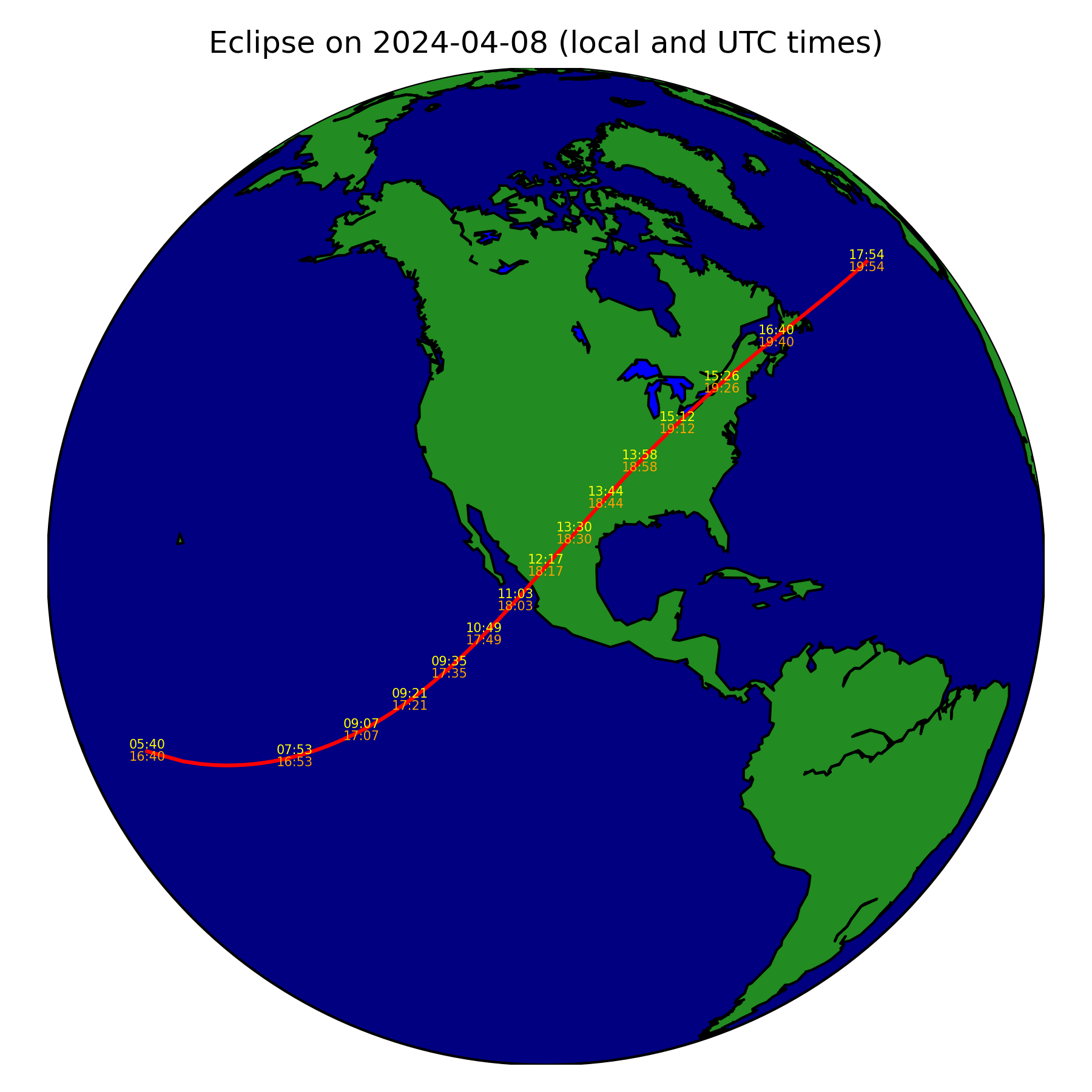
Gorgeous!

Actually this probably isn't award-winning in terms of design quality, but it feels fairly decent for something as a starting point — the point here isn't necessarily to win design awards, but to find eclipses in ~100 lines of Python.

Which the script does! In fact, it finds all the eclipses in the 2020-2030 period:

• 2020-06-21 over Africa, Middle East, and Asia
• 2020-12-14 over a tiny bit of South America
• 2021-06-10 over northern Canada and Greenland
• 2021-12-04 over Antarctica
• 2023-04-20 over Australia and Papua New Guinea
• 2023-10-14 over USA, Central America, and South America
• 2024-04-08 over Mexico, USA and Canada (tomorrow!!)
• 2024-10-02 over a tiny bit of South America (again?)
• 2026-02-17 over a tiny bit of Antarctica (will anyone see it?)
• 2026-08-12 over Greenland and Spain
• 2027-02-06 over a tiny bit of South America (a third time??)
• 2027-08-02 over North Africa and Middle East
• 2028-01-26 over South America and Spain
• 2028-07-22 over Australia and New Zealand

This does indeed look identical to other lists I found online, which is quite reassuring.

Total runtime is a few minutes thanks to Modal.

It is admittedly a bit of a brute-force approach to do it this way, and I'm sure NASA has a version in C++ that runs 1000 times faster. However, the brute-force approach is such a obvious winner in terms of developer productivity, even ignoring the fact that we also plotted maps!

Notes

• Lucky bastards in the south of South America catching three eclipses in a decade.
• The code is here if you want to check it out!.
• I was somewhat inspired by this blog post doing something similar in Mathematica and I guess I have to say I'm impressed with the amount of eclipse-related functions in Mathematica?
• Credits to Stackoverflow code here for a starting point in my code
• I ignored the difference between annular and total eclipses in my code, although this probably isn't super hard to fix.
• I also didn't compute the width of the path of totality, i.e. the width of the sun's shadow on the Earth. Just the path of the center of that shadow.